Introduction
Trends across a period follow from the increasing
number of protons in the nucleus and the decrease in radius.
Both contributions can be explained by the change in
effective nuclear charge.
Trends down a group follow from the increasing number of
electron shells and the increased distance of the outer electrons
from the nucleus. The major factor is the increasing size.
The properties of an element are largely determined by their electronic
configurations, giving rise to recurring patterns or periodic behaviour.
Examples are shown in the diagrams below including ionization energy,
electron affinity, electronegativity and atomic radii. It is this periodicity
of properties, manifestations of which were noticed well before the underlying
theory was known, that led to the establishment of the periodic law (the
properties of the elements recur at varying intervals) and the development
of the first periodic tables. The modern periodic table is a tabular
arrangement of the chemical elements, organized on the basis of their
atomic number (number of protons in the nucleus), electronic configurations,
and recurring chemical properties.
In
the RSC Tutorial Chemistry Text on Main Group Chemistry, it notes that
"When an element forms a chemical compound, electrons can be considered to be
either lost, gained or shared with other atoms. These tendencies can be
assessed by the parameters of ionization energy (IE), electron affinity (EA)
and electronegativity (E). Prediction of bond types as either ionic or covalent then
allows prediction of the chemical and physical properties of chemical substances."
So how are these parameters defined and how do they vary with atomic number?
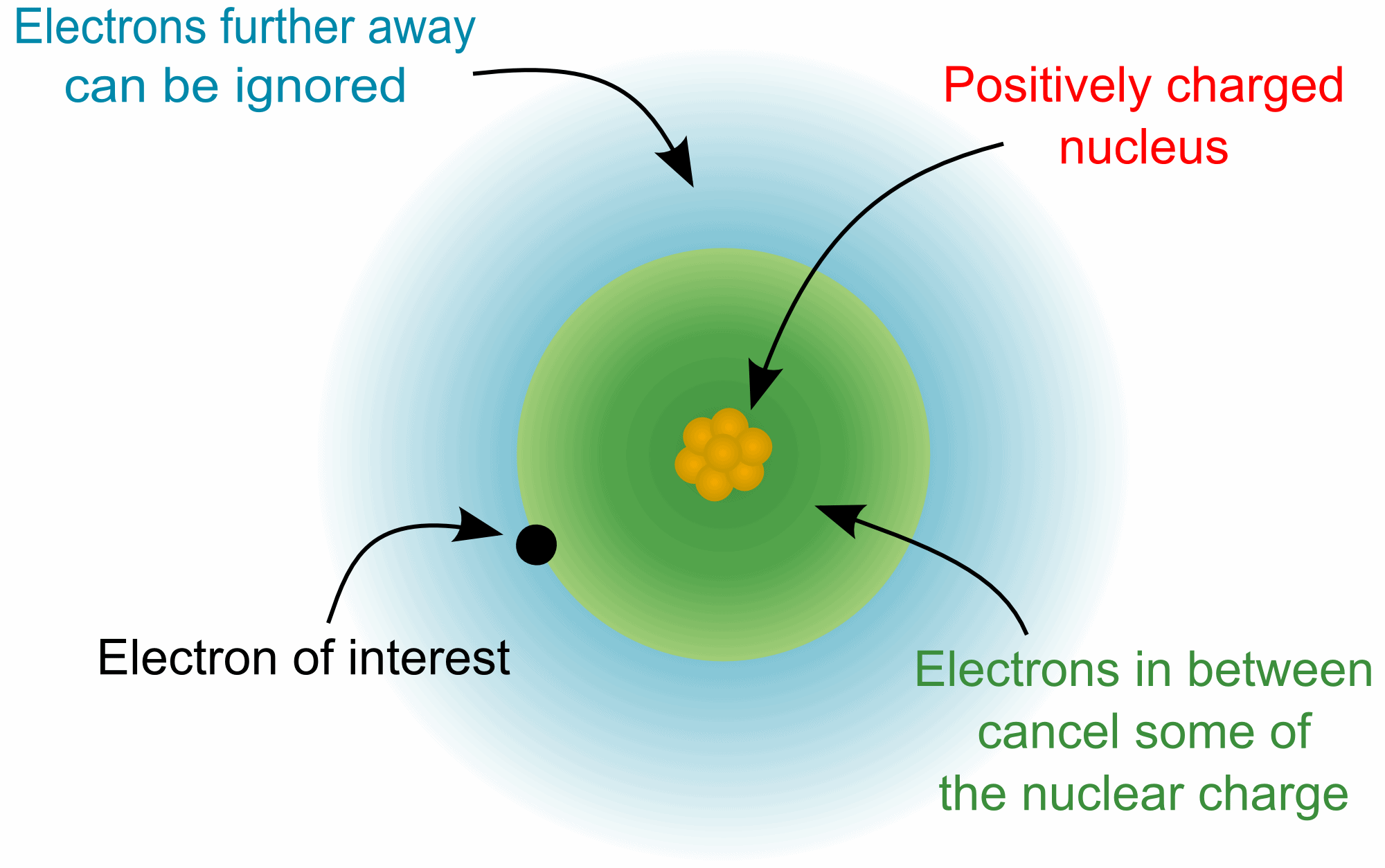
The concept of the effective nuclear charge (often symbolized as
Zeff or Z*) relates to the net positive charge experienced by
an electron in a multi-electron atom. The term "effective" is used because
the shielding effect of negatively charged inner electrons prevents higher
orbital electrons from experiencing the full nuclear charge due to the
repelling effect of the lower inner-layer electrons.
In an atom with one electron, that electron experiences the full charge
of the positive nucleus. In this case, the effective nuclear charge can be
calculated from Coulomb's law.
However, in an atom with many electrons the outer electrons are
simultaneously attracted to the positive nucleus and repelled by the inner
negatively charged electrons. The effective nuclear charge on such an
electron is given by the following equation:
Zeff = Z - S
where
Z is the number of protons in the nucleus (atomic number), and
S is the shielding calculated from the electrons between the nucleus and the
electron in question. A systematic method for determining this is given by
"Slater's rules".
These can be summarised as follows:
Arrange the electrons into a sequence of groups in order of increasing
principal quantum number n, and for equal n in order of increasing
azimuthal quantum number l, except that s- and p- orbitals are kept together.
[1s] [2s,2p] [3s,3p] [3d] [4s,4p] [4d] [4f] [5s, 5p] [5d] etc.
Any electron higher in the sequence to the electron under consideration
contributes nothing to the shielding, S, and is ignored.
For an electron in an ns or np orbital:
0.35 comes from each other electron within the same group except for
the [1s] group, where the other electron contributes only 0.30.
0.85 for each electron with principal quantum number n one less than
that of the group, i.e (n-1) shell
1.00 for each electron with principal quantum number two or more less,
i.e (n-2) etc. shell
For an electron in an nd or nf orbital:
0.35 comes from each other electron within the same group
1.00 for each electron "closer" to the atom than the group. This includes
electrons with the same principal quantum number but in s or p orbitals.
In tabular form, the rules are summarized as:
| Group |
Other electrons in the same group |
Electrons in group(s) with principal quantum number n and azimuthal quantum number < l |
Electrons in group(s) with principal quantum number n-1 |
Electrons in all group(s) with principal quantum number < n-1 |
| [1s] |
0.30 |
- |
- |
- |
| [ns, np] |
0.35 |
- |
0.85 |
1 |
| [nd] or [nf] |
0.35 |
1 |
1 |
1 |
Example 1.
Consider a sodium cation, Na+, a fluorine anion, F-,
and a neutral neon atom, Ne. Each has 10 electrons,
1s2 2s2 2p6 so the shielding from the 1s
and 2s/2p electrons is 2 * 0.85 + 7 * 0.35 = 4.15 but the effective nuclear
charge varies because each has a different atomic number:
Zeff F- = 9 - 4.15 = 4.85
Zeff Ne = 10 - 4.15 = 5.85
Zeff Na+ = 11 - 4.15 = 6.85
So the sodium cation has the largest effective nuclear charge,
and can be expected to have the smallest radius.
Example 2.
Predict whether K would be more energetically stable with a configuration of
1s2 2s2 2p6 3s2 3p6 4s1
or
1s2 2s2 2p6 3s2 3p6 3d1
For K, Z=19 and considering the 4s electron then the screening constant S
can be calculated from:
S= (8 * 0.85) + (10 * 1.0) = 16.8
Zeff = 19 - 16.8 = 2.2
For the 3d calculation of S:
S= (18 * 1.0) = 18
Zeff = 19 - 18 = 1
Accordingly, an electron in the 4s (as opposed to the 3d) orbital
would come under the influence of a greater effective nuclear charge in
the ground state of potassium and so will be the orbital that is occupied.
The Ionization Energy (IEn) of an element is defined as the
internal energy change associated with the removal of an electron from the
gaseous atom, E, in its ground state, i.e. at 0 K.
The first IE is therefore the energy required for the reaction:
E(g) → E+(g) + e- energy required = IE
This energy change is generally considered equivalent to the enthalpy change at 298 K
(ΔH298 K).
Estimates of the error suggest < 10 kJmol-1 which when compared
to typical IE values often in their thousands, is insignificant.
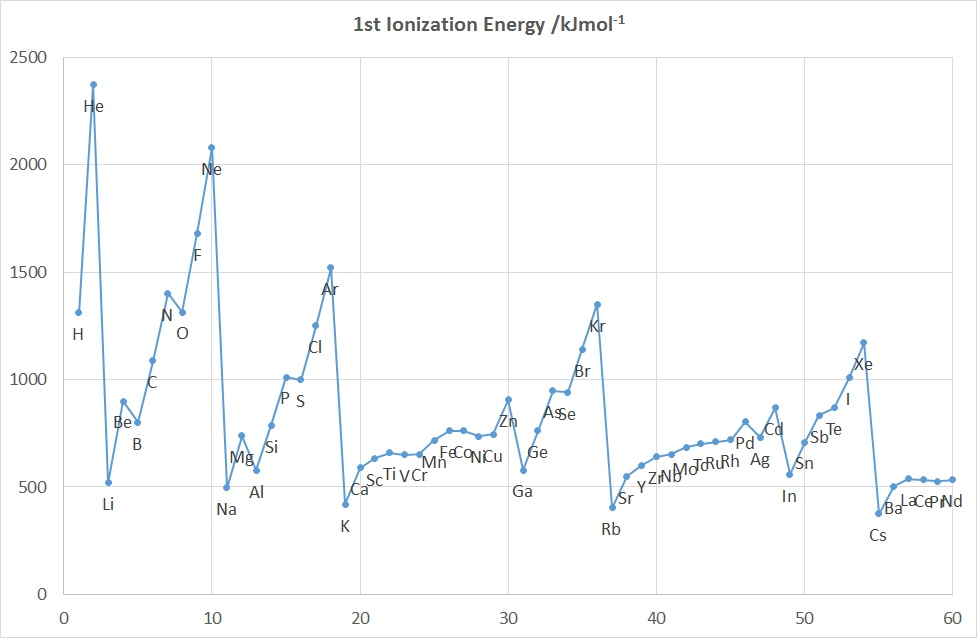
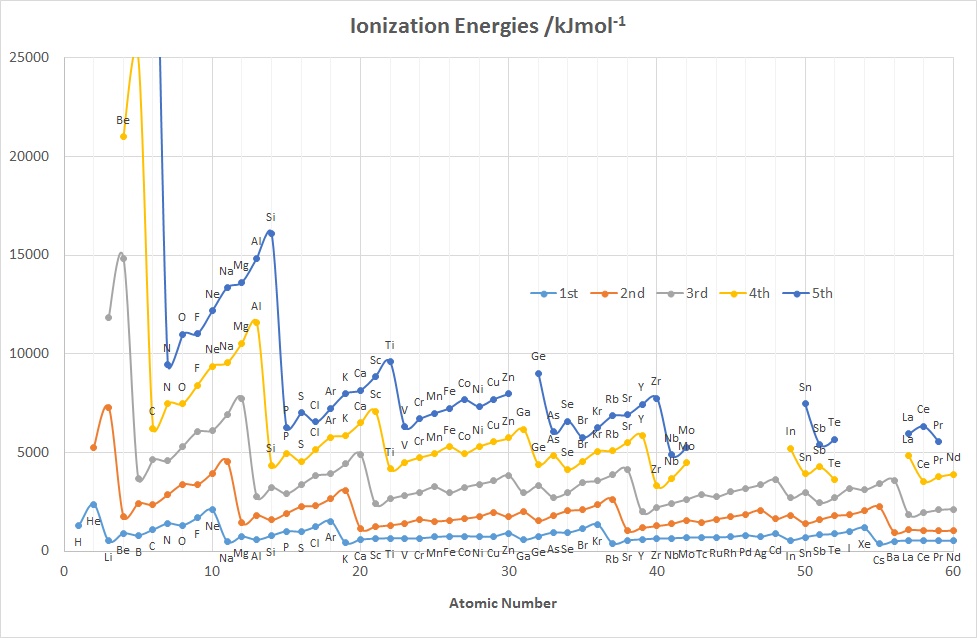
The diagrams above show the variation in the values of the 1st five
IE's as a function of Z up to Nd (60).
Features to note for IE1 are:
- the values associated with the noble gases are the highest in each period
- the values associated with the group 1 elements are generally the lowest
in each period, (group 2 elements for the 2nd IE and group 3 for the 3rd IE etc.)
- the gradual increase in values across a given period (applies to
IE2-5 as well)
- the drop in values on going from an element in group 15
to its neighbour in group 16 e.g. for N-O, P-S, As-Se
- the drop in values on going from an element in group 2 or 12 to its
neighbour in group 13, e.g. for Be-B, Mg-Al and Zn-Ga, Cd-In
- the rather similar values for a given row of d-block elements
These observations can be accounted for in terms of the effective nuclear charge
since the further away from the positively charged nucleus that a negatively charged
electron is located, the less strongly that electron is attracted to the
nucleus and the more easily it can be removed. So, as the atomic radius
decreases from left to right across the Period the 1st Ionization Energy
increases.
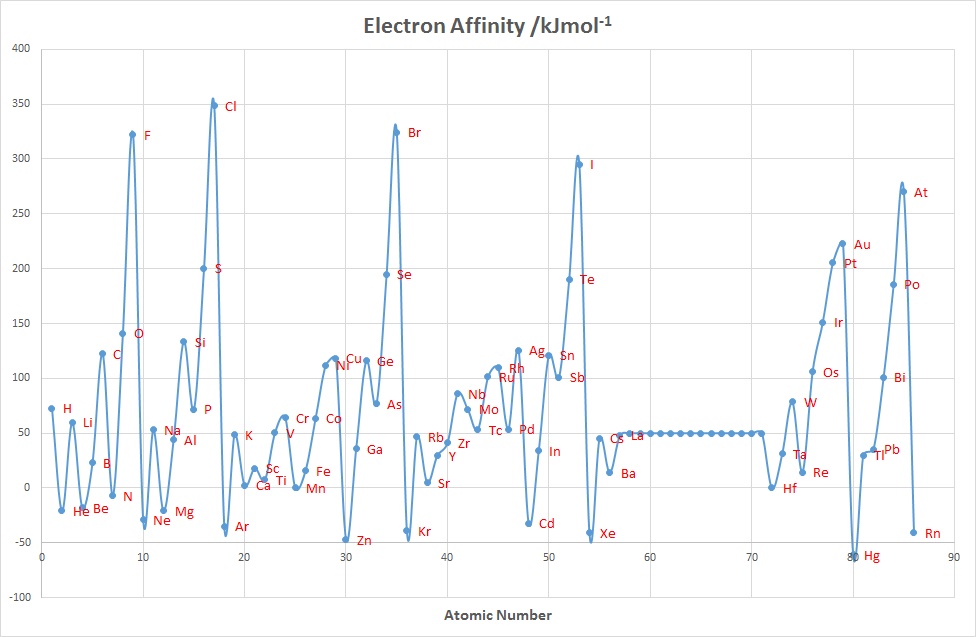
Electron Affinity
The electron affinity(EA) of an element E is defined as minus the internal
energy change associated with the gain of an electron by a gaseous atom, at 0 K :
E(g) + e- → E-(g)
energy change = ΔEAU(0 K)
This energy change is generally considered to be equivalent to
ΔH298 K, so:
EA = - ΔH298 K
Unlike ionization energies, which are always positive for a neutral atom
because energy is required to remove an electron, electron affinities
can be positive (energy is released when an electron is added),
negative (energy must be added to the system to produce an anion),
or zero (the process is energetically neutral).
Chlorine has the most positive electron affinity of any element,
which means that more energy is released when an electron is added to
a gaseous chlorine atom than to an atom of any other element, EA= 348.6 kJmol-1
and the group 17 elements have the largest values overall. The addition of a
second electron to an element is expected to be much less favoured since
there will be repulsion between the negatively charged electron and the overall
negatively charged anion. For example, for O the values are:
O(g) + e → O-(g) EA = + 141 kJmol-1
O-(g) + e → O2-(g) EA = - 798 kJmol-1
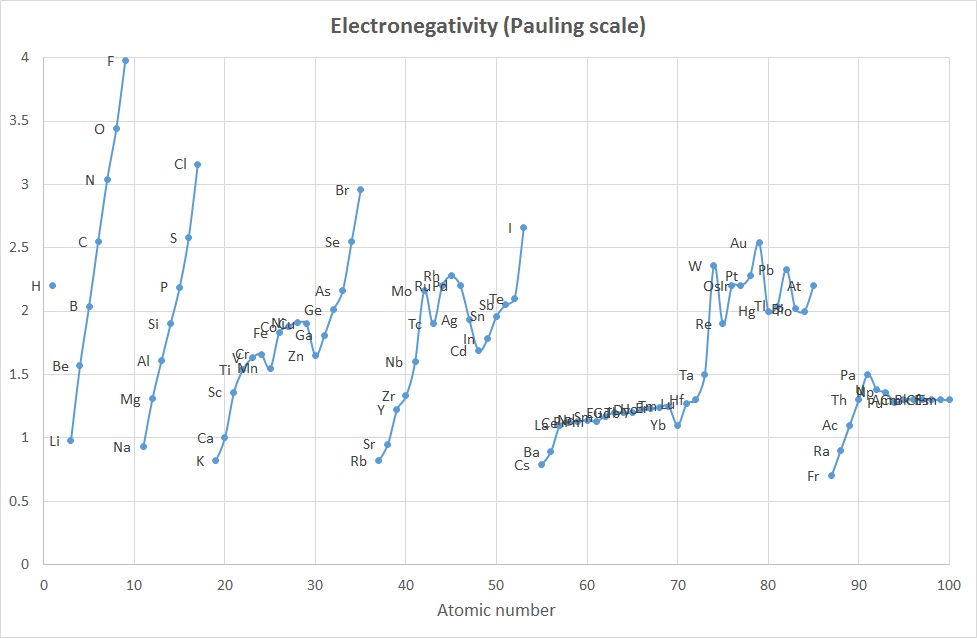
The concept of Electronegativity originated with Linus Pauling in the 1930's
and was defined as "the power of an atom in a molecule to attract electrons
to itself".
The values proposed by Pauling were calculated based on differences in
bond dissociation enthalpy values found
when comparing homo-diatomic molecues with hetero-diatomic molecules.
For example , the bond energy of chlorine monofluoride, ClF, is about
255 kJ mol-1 which is significantly greater than for either
of the two homo-nuclear species Cl2 and F2 (242 and 153
kJ mol-1 respectively). Pauling attributed this to an
electrostatic attraction between the partially charged atoms in the
heternuclear species. That is the excess bond energy came from an
ionic contribution to the bond.
The method of calculating the Pauling values is:
D(XY) = [D(XX).D(YY)]1/2 + 96.48 * (χY - χX)2
where the 96.48 factor means D values are in kJ mol-1
In Housecroft and Sharpe the average, rather than geometric mean is used,
and this is rearranged to give:
ΔD = D(XY) - {½ * [D(XX) - D(YY)] } = (χY - χX)2
= (Δχ)2
or Δχ = √(ΔD)
As only differences in electronegativity were defined, it was necessary
to choose an arbitrary reference point in order to construct a scale.
Hydrogen was chosen as the reference, since it formed covalent bonds with
a large variety of elements: its electronegativity was fixed at 2.20.
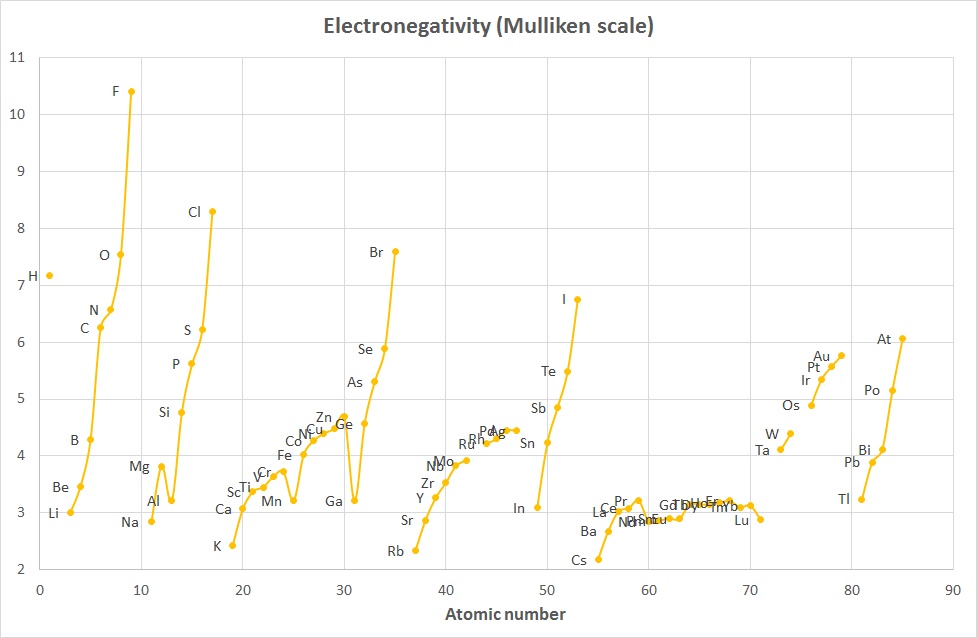
The Mulliken scale was calculated by taking the average of
the Ionization Energy and the Electron Affinity (when both were given in
units of eV).
χM = ½ (IE1 + EA1)
where both IE1 and EA1 are in eV
A variant of this (2006) that converts the values to roughly the Pauling scale is:
χM = 0.00197 * (IE1 + EA1) + 0.19
where IE1 and EA1 are now given
in kJ mol-1
The plots above indicate that while the absolute values are different, the trends
are quite similar and the 2 curves are comparable when scaled appropriately.
The Allred-Rochow scale considered that electronegativity
was related to the charge experienced by an electron on the "surface"
of an atom: the higher the charge per unit area of atomic surface
the greater the tendency of that atom to attract electrons.
Their scale was dependent on Zeff and inversely
proportional to the square of the covalent radius, rcov.
χAR = (3590 * Zeff / r2cov)
+ 0.744 where rcov is in pm
The values range between 0 and 10. Once again a good correlation to the
Pauling scale was found and this applies as well to other
Electronegativity scales.
Atomic Radius
Have a look at an interactive visual display (JSmol) showing the
periodic table of elements with atomic and ionic radii.
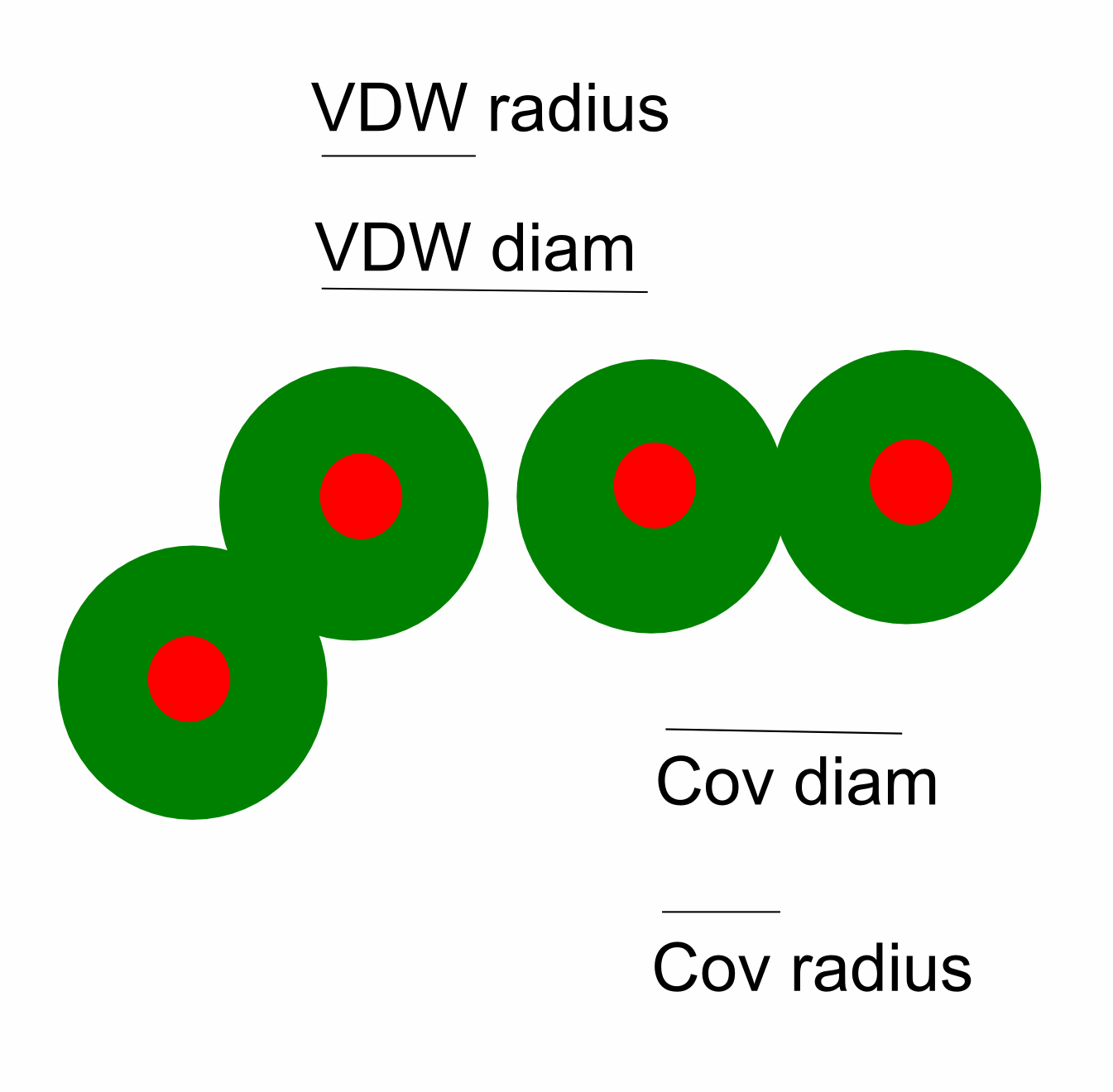
The atomic radius of a chemical element is a measure of the size of its
atoms, usually the mean or typical distance from the center of the nucleus
to the boundary of the surrounding cloud of electrons. Since the boundary is
not a well-defined physical entity, there are various non-equivalent
definitions of atomic radius. Three widely used definitions of atomic radius
are Van der Waals radius, ionic radius, and covalent radius.
Covalent radius is defined as half the covalent bond length
when the two atoms bonded are homonuclear (½ X-X bond).
van der Waals radius is defined as half of the internuclear
separation of two non-bonded atoms of the same element on their closest
possible approach.
It is not possible to measure the sizes of both metallic and nonmetallic
elements using a single technique and method. To get values for comparison,
theoretical quantum mechanical functions have been used instead to
calculate atomic radii.
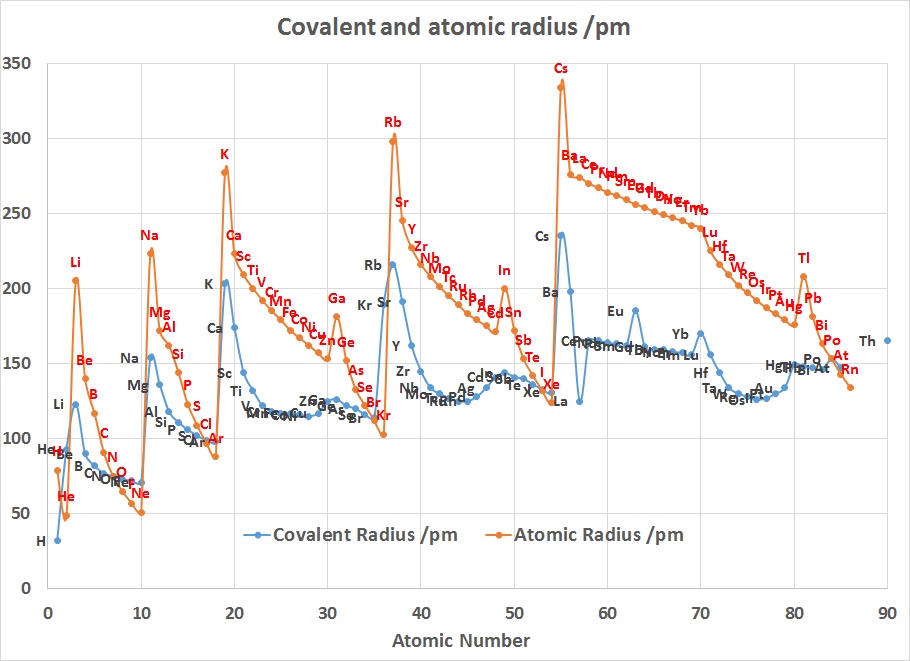
In the periodic table, atomic radii decrease from left to right across a
period and increase from top to bottom down the groups. As a result of these
two trends, the largest atoms are found in the lower left corner of the
periodic table, and the smallest are found in the upper right corner.
The radius increases sharply between the noble gas at the end of each period
and the alkali metal at the beginning of the next period. These trends of the
atomic radii (and of various other chemical and physical properties of the
elements) can be explained by the electron shell theory of the atom; they
provided important evidence for the development and confirmation of
quantum theory. The atomic radii decrease across the Periodic Table
because as the atomic number increases, the number of protons increases
across the period, but the extra electrons are only added to the same
quantum shell. Therefore, the
effective nuclear charge towards the outermost
electrons increases, drawing the outermost electrons closer. As a result,
the electron cloud contracts and the atomic radii decreases.
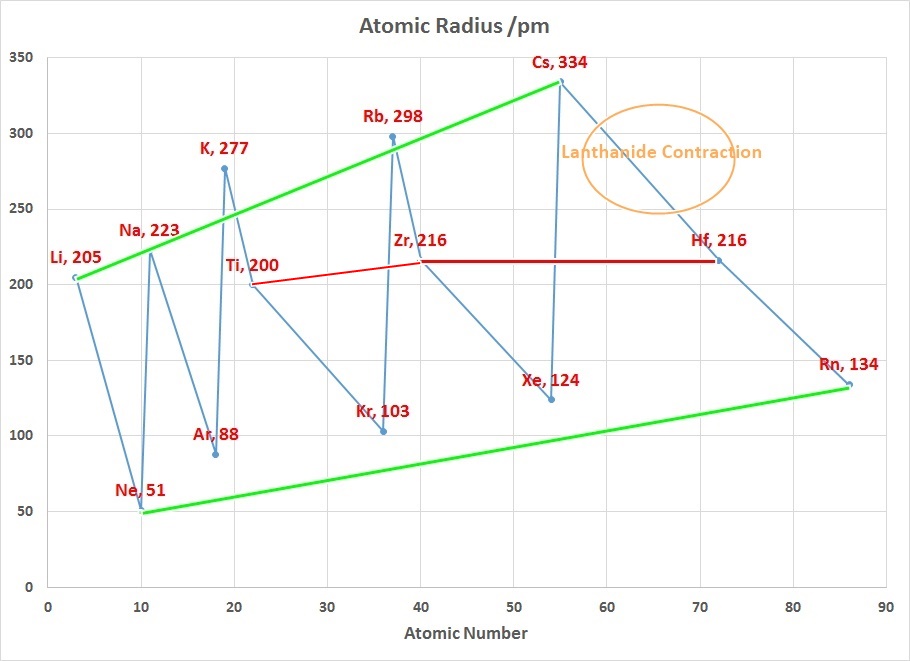
The Lanthanide Contraction
The chart on the right above can be used to explain why Zirconium and Hafnium
are two of the hardest elements in the Periodic Table to separate. In addition
why the teaching of Transition Metal Chemistry is often covered in 2 courses
since the properties of the first row elements are expected to be quite
different to those of the second and third row.
Considering that the size of Gallium is smaller than Aluminium suggests
that the 3d contraction is having an impact as well.
Although neither atoms nor ions have sharp boundaries, they are sometimes
treated as if they were hard spheres with radii such that the sum of ionic
radii of the cation and anion gives the distance between the ions in a
crystal lattice.
Ions may be larger or smaller than the neutral atom, depending on the
ion's charge. When an atom loses an electron to form a cation, the lost
electron no longer contributes to shielding the other electrons from
the charge of the nucleus; consequently, the other electrons are more
strongly attracted to the nucleus, and the radius of the atom gets smaller.
Similarly, when an electron is added to an atom, forming an anion, the added
electron shields the other electrons from the nucleus, with the result
that the size of the atom increases. Typical values range from 50 pm to
over 220 pm.
Return to the
course outline
or move on to Lecture 2:
Polarizing power and polarizability, Anomalous behavior of row 2 elements.
References
Much of the information in these course notes has been sourced from Wikipedia under
the Creative Commons License.
'Main Group Chemistry'- W Henderson, RSC, 2000, DOI:10.1039/9781847551283
'Inorganic Chemistry' - C. Housecroft and A.G. Sharpe, Prentice Hall, 4th Ed.,
2012, ISBN13: 978-0273742753, pps 24-27, 43-50, 172-176, 552-558, 299-301, 207-212
Free on-line edition of a General Chemistry text
'Basic Inorganic Chemistry' - F.A. Cotton, G. Wilkinson and P.L.
Gaus, John Wiley and Sons, Inc. 3rd Ed., 1994.
'Introduction to Modern Inorganic Chemistry' - K.M. Mackay, R.A.
Mackay and W. Henderson, International Textbook Company, 5th Ed., 1996.

This work is licensed under a Creative Commons
Attribution-ShareAlike 3.0 Unported License.
 Return to Chemistry,
UWI-Mona, Home Page
Created and maintained by Prof. Robert J.
Lancashire,
Return to Chemistry,
UWI-Mona, Home Page
Created and maintained by Prof. Robert J.
Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica
Created November 2014. Links checked and/or last
modified 31st January 2015.
URL
http://wwwchem.uwimona.edu.jm/courses/CHEM1902/IC10K_MGtrends.html


 Return to Chemistry,
UWI-Mona, Home Page
Created and maintained by Prof. Robert J.
Lancashire,
Return to Chemistry,
UWI-Mona, Home Page
Created and maintained by Prof. Robert J.
Lancashire,