Introduction to the colour and magnetism of 1st row transition metal complexes
Before beginning a more detailed examination of the spectroscopy and magnetism of
transition meal complexes, it is worth while reviewing how far a simple CFT
approach will take us.
When electromagnetic radiation is absorbed by atoms or molecules it promotes
them to an excited state. Microwave and infrared radiation correspond to lower
energy quanta and so initiate rotational and vibrational excitation. Visible and
UV light have much higher frequencies and can cause excitations characterstic
of electronic excitation: the promotion of an electron from one orbital
to another. We expect therefore that molecules will absorb light when the
energy corresponds to the energy differences between occupied and unoccupied
orbitals. For transition metal ions, the simplest case is Ti(III), solutions
of which appear violet.
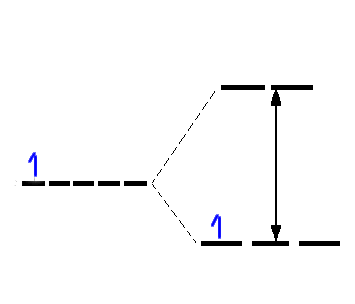
Absorption of light of frequency ~20,000 cm-1 excites the electron from the t2g
subset to the eg subset. This is described as a eg ← t2g transition.
Absorption of green light, i.e. transmission of blue and red, gives
a purple solution
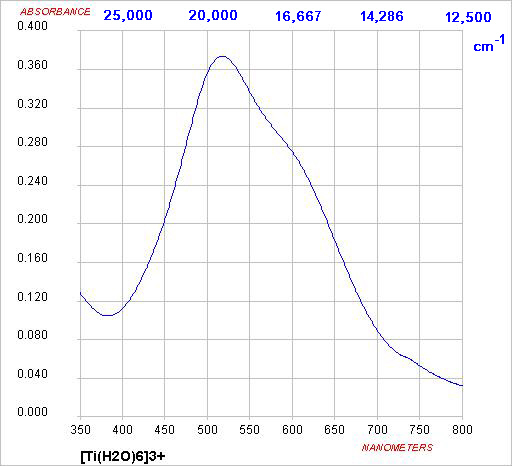
ν ~20,000 cm
-1
λ
max ~ 500 nm
E = hν = hc/λ
Δ ~ 240 kJ mol
-1
Rough guide to absorbance and colour
| Wavelength Absorbed (nm) |
Frequency (cm-1) |
Colour of Light Absorbed |
Colour of Complex |
| 410 |
24,400 |
violet |
lemon-yellow |
| 430 |
23,300 |
indigo |
yellow |
| 480 |
20,800 |
blue |
orange |
| 500 |
20,000 |
blue-green |
red |
| 530 |
18,900 |
green |
purple |
| 560 |
17,900 |
lemon-yellow |
violet |
| 580 |
17,200 |
yellow |
indigo |
| 610 |
16,400 |
orange |
blue |
| 680 |
14,700 |
red |
blue-green |
In spectroscopy it is usual to measure either the amount of light
that is absorbed or transmitted through the sample. For UV/Vis,
absorbance is given by the Beer-Lambert expression:
A = ε c l
where A is the Absorbance
ε is the molar absorbance (extinction coefficient)
c is the concentration
and l is the path length of the cell
The most common (and cheapest) sample cells have a 1 cm path length and since A
is unitless then we can see that the units of ε are
mol-1 l cm-1. To move this to an acceptable
SI set of units requires converting ε to units of
m2 mol-1 and this involves a factor of 1/10.
Thus an ε of 5 mol-1 l cm-1 is
equivalent to ε of 0.5 m2 mol-1.
Given that the separation between the t2g and eg levels
is Δ then whether there is 1 d electron or several d electrons the simple
Crystal Field Theory model would suggest that there is only 1 energy gap hence all
spectra should consist of 1 peak. That this is not found in practise means that
the theory is not sophisticated enough. What is required is an extension of
the theory that allows for multi-electron systems where the energy levels
are modified to include electron-electron interactions. This can be achieved
by looking at the various quantum numbers for each of the electrons involved
and using a system called the Russell-Saunders
coupling scheme to describe an electronic state that can adequately
describe the energy levels available to a group of electrons that includes
these interactions.
Magnetism
In CHEM1902 (C10K) we introduced the formula used to relate the magnetic moment
to the number of unpaired spins in a transition metal complex.
μs.o. = √{4S(S+1)} B.M.
During the laboratory session you will carry out a measurement of the
magnetic susceptibility which is a measure of the force exerted by the
magnetic field on a unit mass of the sample under investigation. This
is related to the number of unpaired electrons per unit weight and
hence per mole and in the simplest picture we consider that this
is solely dependent on the presence of unpaired electrons.
For a Ti(III) complex with 1 unpaired electron this corresponds to:
μs.o. = 2 √ (1/2 (1/2 + 1)) B.M
μs.o. = √ (3) B.M.
μs.o. = 1.73 Bohr Magneton
We will see later that while the spin-only approximation works in many cases,
for a more complete analysis it is necessary to consider the contribution
made by the orbital motion of the electron as well.
return to the CHEM2101 (C21J) course
outline
 Return to Chemistry, UWI-Mona,
Home Page
Return to Chemistry, UWI-Mona,
Home Page
Copyright © 2006-2010 by Robert John
Lancashire, all rights reserved.
Created and maintained by Prof. Robert J.
Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.
Created Sep 2006. Links checked and/or last
modified 16th September 2010.
URL
http://wwwchem.uwimona.edu.jm/courses/SpecIntro.html


 Return to Chemistry, UWI-Mona,
Home Page
Return to Chemistry, UWI-Mona,
Home Page