Calculations using Orgel diagrams
Orgel diagrams are useful for showing the energy levels of both
high spin octahedral and tetrahedral transition metal ions. They
ONLY show the spin-allowed transitions.
For complexes with D ground terms only one electronic transition
is expected and the transition energy corresponds directly to
Δ. Hence, the following high spin
configurations are dealt with: d1, d4,
d6 and d9.
D Orgel diagram
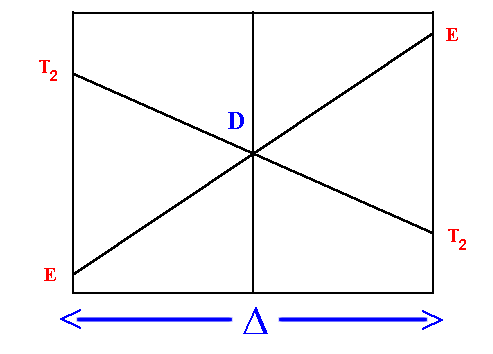
On the left hand side d1, d6 tetrahedral
and d4, d9 octahedral complexes are covered
and on the right hand side d4, d9
tetrahedral and d1, d6 octahedral.
For simplicity, the g subscripts required for the octahedral
complexes are not shown.
For complexes with F ground terms, three electronic transitions
are expected and Δ may not correspond
directly to a transition energy. The following configurations are
dealt with: d2, d3, high spin d7
and d8.
F Orgel diagram
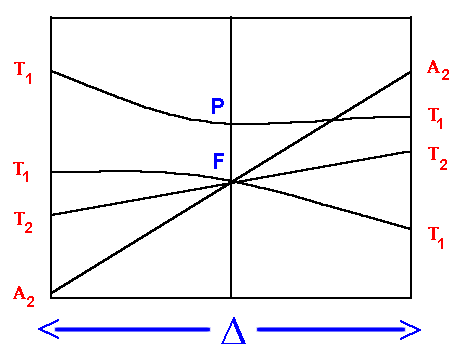
On the left hand side, d2, d7 tetrahedral
and d3, d8 octahedral complexes are covered
and on the right hand side d3, d8
tetrahedral and d2 and high spin d7
octahedral.
Again for simplicity, the g subscripts required for the
octahedral complexes are not shown.
On the left hand side, the first transition corresponds to Δ,
the equation to calculate the second
contains expressions with both Δ and C.I.
(the configuration interaction from repulsion of like terms) and
the third has expressions which contain Δ, C.I. and the Racah parameter B.
- 4T2g ← 4A2g
transition energy = Δ
- 4T1g(F) ← 4A2g
transition energy = 9/5 * Δ - C.I.
- 4T1g(P) ← 4A2g
transition energy = 6/5 * Δ + 15B' + C.I.
On the right hand side,
The first transition can be unambiguously assigned as:
3T2g ← 3T1g
transition energy = 4/5 * Δ + C.I.
But, depending on the size of the ligand field (Δ)
the second transition may be due to:
3A2g ← 3T1g
transition energy = 9/5 *Δ + C.I.
for a weak field or
3T1g(P) ← 3T1g
transition energy = 3/5 * Δ + 15B' + 2 * C.I.
for a strong field.
TANABE-SUGANO DIAGRAMS
An alternative method is to use Tanabe Sugano diagrams, which are
able to predict the transition energies for both spin-allowed and
spin-forbidden transitions, as well as for both strong field (low
spin), and weak field (high spin) complexes.
Note however that most textbooks only give Tanabe-Sugano diagrams
for octahedral complexes and a separate diagram is required for
each configuration.
In this method the energy of the electronic states are given on
the vertical axis and the ligand field strength increases on the
horizontal axis from left to right.
Linear lines are found when there are no other terms of the same
type and curved lines are found when 2 or more terms are
repeated. This is as a result of the "non-crossing rule".
The baseline in the Tanabe-Sugano diagram represents the lowest
energy or ground term state.
The d2 case (not many examples
documented).
The electronic spectrum of the V3+ ion, where V(III)
is doped into alumina (Al2O3), shows three
major peaks with frequencies of: ν1=17400
cm-1, ν2=25400 cm-1
and ν3=34500 cm-1.
These have been assigned to the following
spin-allowed transitions.
| 3T2g |
<--- |
3T1g |
| 3T1g(P) |
<--- |
3T1g |
| 3A2g |
<--- |
3T1g |
The ratio between the first two transitions is calculated as
ν2 / ν1 which is equal to 25400 / 17400 = 1.448.
In order to calculate the Racah parameter, B,
the position on the horizontal axis where the ratio between the
lines representing ν2 and ν1 is equal to 1.448, has to be determined. On
the diagram below, this occurs at Δ/B=30.9. Having found this value,
a vertical line is drawn at this position.
Tanabe-Sugano diagram for d2 octahedral complexes
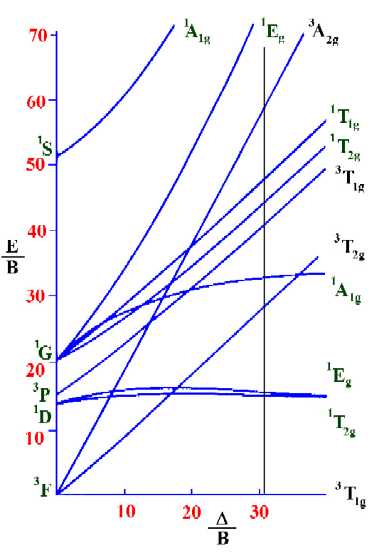
On moving up the line from the ground term to where lines from
the other terms cross it, we are able to identify both the
spin-forbidden and spin-allowed transition and hence the total
number of transitions that are possible in the electronic
spectrum.
Next, find the values on the vertical axis that correspond to the
spin-allowed transitions so as to determine the values of ν1/B, ν2/B and
ν3/B. From the diagram above these are 28.78, 41.67 and 59.68 respectively.
Knowing the values of ν1, ν2 and ν3, we can now
calculate the value of B.
Since ν1/B=28.78 and ν1 is equal to 17,400 cm-1, then
B=ν1/28.78 = 17400/28.78
or B=604.5cm-1
Then it is possible to calculate the value of Δ.
Since Δ/B=30.9, then: Δ=B*30.9 and hence: Δ =
604.5 * 30.9 = 18680 cm-1
The d3 case
Calculate the value of B and Δ for the Cr3+ ion in
[Cr(H2O)6)]3+ if ν1=17000 cm-1,
ν2=24000 cm-1 and ν3=37000 cm-1.
SOLUTION.
These values have been assigned to the following
spin-allowed transitions.
| 4T2g |
<--- |
4A2g |
| 4T1g |
<--- |
4A2g |
| 4T1g(P) |
<--- |
4A2g |
Using a Tanabe-Sugano diagram for a d3 system this ratio is found
at Δ/B=24.00
Tanabe-Sugano diagram for d3 octahedral complexes
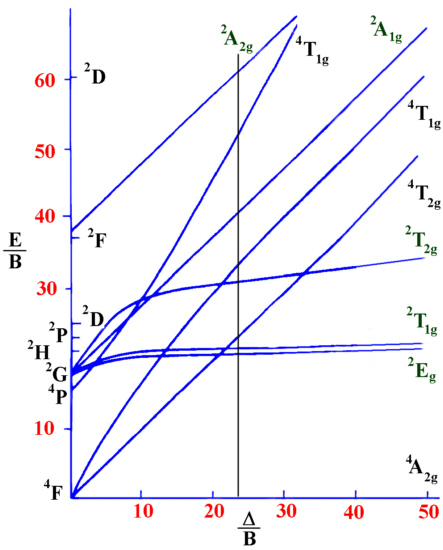
ν1/B=24.00
ν2/B=33.90
ν3/B=53.11
Recall that ν1=17000 cm-1.
Therefore for the first spin-allowed transition,
17000 /B =24.00 from which B can be obtained, B=17000 / 24.00 or
B=708.3 cm-1.
This information is then used to calculate Δ.
Since Δ / B=24.00 then Δ = B*24.00 = 708.3 * 24.00 = 17000
cm-1.
It is observed that the value of Racah parameter B in the
complex is 708.3 cm-1, while the value of B in the
free Cr3+ ion is 1030cm-1. This shows a 31%
reduction in the Racah parameter indicating a strong
Nephelauxetic effect.
The Nephelauxetic Series is as follows:
F->H2O>urea>NH3
>en~C2O42-
>NCS-
>Cl-~CN->Br-
>S2- ~I-.
Ionic ligands such as F-give small reduction in B,
while covalently bonded ligands such as I- give a
large reduction in B.
Note
The original paper by Tanabe and Sugano[10] had the d5
and d6 diagrams each missing a T term from excited I
states. These diagrams were reproduced in the often quoted text
by Figgis[12(a)] and so the errors have been perpetuated. An
exception is the text by Purcell and Kotz[15] where the missing T
terms have been included, however in their case they have ignored
lower lying terms from excited D, F, G and H states which for
d5 are the main transitions seen in the spin forbidden
spectra of Mn(II) complexes.
A set of qualitative diagrams have been
drawn for each configuration (which include the missing T terms)
and along with the newest release of "Ligand Field Theory and its applications"
by Figgis and Hitchman [12(b)] represent the only examples of Tanabe-Sugano diagrams
that provide a comprehensive set of terms for spectral interpretation.
References
1. Basic Inorganic Chemistry, F.A.Cotton, G.Wilkinson and
P.L.Gaus, 3rd edition, John Wiley and Sons, Inc. New York,
1995.
2. Physical Inorganic Chemistry, S.F.A.Kettle, Oxford University
Press, New York, 1998.
3. Complexes and First-Row Transition Elements, D.Nicholls,
Macmillan Press Ltd, London 1971.
4. The Chemistry of the Elements, N.N.Greenwood and A.Earnshaw,
Pergamon Press, Oxford, 1984.
5. Concepts and Models of Inorganic Chemistry, B.E.Douglas,
D.H.McDaniel and J.J.Alexander 2nd edition, John Wiley &
Sons, New York, 1983.
6. Inorganic Chemistry, J.A.Huheey, 3rd edition, Harper &
Row, New York, 1983.
7. Inorganic Chemistry, G.L.Meissler and D.A.Tarr, 2nd edition,
Prentice Hall, New Jersey, 1998.
8. Inorganic Chemistry, D.F.Shriver and P.W.Atkins, 3rd edition,
W.H.Freeman, New York, 1999.
9. Basic Principles of Ligand Field Theory, H.L.Schlafer and
G.Gliemann, Wiley-Interscience, New York, 1969.
10. Y.Tanabe and S.Sugano, J. Phys. Soc. Japan, 9, 1954, 753 and
766.
11(a). Inorganic Electronic Spectroscopy, A.B.P.Lever, 2nd
Edition, Elsevier Publishing Co., Amsterdam, 1984.
11(b). A.B.P.Lever in Werner Centennial, Adv. in Chem Series,
62, 1967, Chapter 29, 430.
12(a). Introduction to Ligand Fields, B.N.Figgis, Wiley, New York,
1966.
12(b). Ligand Field Theory and its applications, B.N. Figgis and
M.A. Hitchman, Wiley-VCH, New York, 2000.
13. E.Konig, Structure and Bonding, 9, 1971, 175.
14. Y. Dou, J. Chem. Educ, 67, 1990, 134.
15. Inorganic Chemistry, K.F. Purcell and J.C. Kotz, W.B.
Saunders Company, Philadelphia, USA, 1977.
 Return to Chemistry,
UWI-Mona, Home Page
Return to Chemistry,
UWI-Mona, Home Page
Copyright © 2019 by Robert John
Lancashire, all rights reserved.
Created and maintained by Prof. Robert J.
Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.
Created February 2000. Links checked and/or last modified
2nd April 2019.
URL
http://wwwchem.uwimona.edu.jm/courses/Tanabe-Sugano/TScalcs.html





 Return to Chemistry,
UWI-Mona, Home Page
Return to Chemistry,
UWI-Mona, Home Page