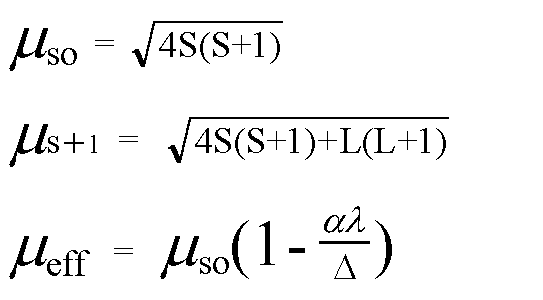Magnetic Moments

Magnetic Moments

Magnetic moments are often used in conjunction with electronic spectra to gain information about the oxidation state and stereochemistry of the central metal ion in coordination complexes.
(Determination of the magnetic moment using the Gouy method has been simplified by the use of an on-line template or spreadsheet.)

For first row transition metal ions in the free ion state, ie isolated ions in a vacuum, all 5 of the 3d orbitals are degenerate.
In octahedral complexes, a simple crystal field theory approach suggests that for these ions the d orbitals are no longer degenerate but are split such that 2 orbitals, the dx2-y2 and the dz2 are at higher energy than the dxy, dxz, dyz.

For ions with between 4 and 7 d electrons, this gives rise to 2 possible arrangements called either high spin-low spin or weak field-strong field respectively. See an interactive JAVA script for examples.

In tetrahedral complexes the orbitals are again split, such that 2 orbitals (the dx2-y2 and the dz2) are now at lower energy than the remaining 3.
Tetrahedral complexes are ALL high spin since the difference between the 2 subsets of orbitals is much smaller than is found in octahedral complexes (Δ_tet= 4/9 Δ_oct).
The formulae most frequently used to calculate magnetic moments of first row transition metal ion complexes are given below:

The first formula is known as the spin only formula, the second takes into account possible contributions from orbital angular momentum and the third is used to make small adjustments when the ground term for the metal ion is either A or E.
Where:
S is the spin quantum number = 1/2 for each unpaired electron
L is the orbital angular momentum
α is a constant = 2 for E and 4 for A ground terms
λ is the spin orbit coupling constant
Δ is the crystal field splitting parameter found from the spectrum of the complex.

To illustrate:
predict the variation of the magnetic moments for the series of tetrahedral complexes Copyr₂Cl₂, Copyr₂Br₂ and Copyr₂I₂.
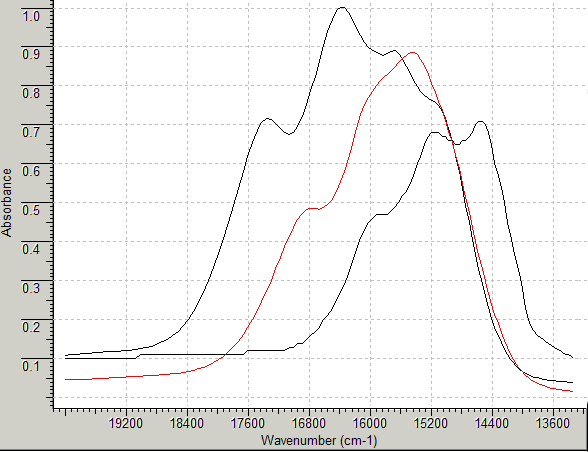
Their visible spectra have been recorded in chloroform

and from the centre of their main absorption bands in the visible region, ν (in wavenumbers cm^-1) can be seen to be roughly:

1 Copyr₂Cl₂ 16260 cm^-1 (615 nm)
2 Copyr₂Br₂ 15870 cm^-1 (630 nm)
3 Copyr₂I₂ 14925 cm^-1 (670 nm)

These peaks represent the third electronic transition expected for these complexes, the other bands occurring in the infrared region, so although we may be able to place the halides into order of the spectrochemical series, we need to consult an Orgel diagram before trying to calculate Δ.
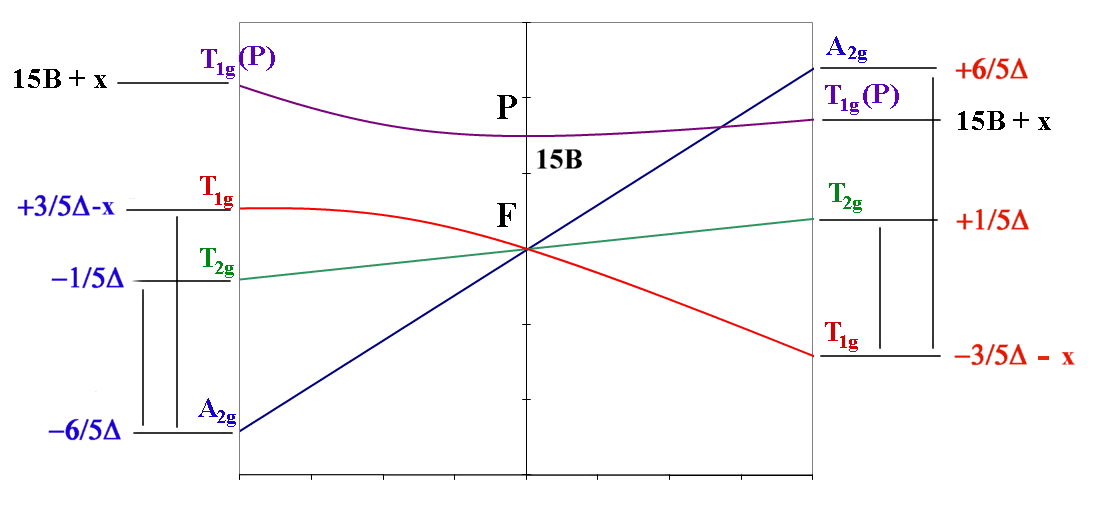
The Orgel diagram appropriate for these types of complexes is given below:

oct d³,d⁸ tet d²,d⁷ ←-----------------------------------→ oct d²,d⁷ tet d³,d⁸

and for d7 tetrahedral the ground term is ⁴A₂.

Three peaks are predicted in their electronic spectra, namely:

⁴T₂    ← ⁴A₂     ν1
⁴T₁(F) ← ⁴A₂     ν2
⁴T₁(P) ← ⁴A₂     ν3 ** the band observed in the visible region

The energy of the third transitions is approximately ν₃ = 6/5 Δ + 15B (where B is the Racah parameter and ignoring configuration interactions). For Co(II) tetrahedral complexes B has generally been found to be about 750 cm^-1.
Hence Δ for the three complexes above can be calculated to be roughly, Δ = (ν₃ - 15x750) x 5/6, or:

Copyr₂Cl₂ (16260-15x750) x 5/6 = 4175 cm^-1
Copyr₂Br₂ (15870-15x750) x 5/6 = 3850 cm^-1
Copyr₂I₂ (14925-15x750) x 5/6 = 3063 cm^-1

For three unpaired electrons the spin only magnetic moment is predicted to be 3.87 BM.
Using a value for the free ion spin orbit coupling constant (λ) of -172 cm^-1 then a better approximation of the magnetic moment can be obtained by using the third formula above. This would give a value of:

Copyr₂Cl₂     3.87*(1+ 688/4175) = 4.49 B.M. found 4.42 BM
Copyr₂Br₂     3.87*(1+ 688/3850) = 4.57 B.M. found 4.50 BM
Copyr₂I₂       3.87*(1+ 688/3063) = 4.76 B.M. found 4.48 BM

In the case of the series;

CoI₄^2-, CoBr₄^2-, CoCl₄^2-, Co(NCS)₄^2-
the magnetic moments have been recorded as
4.77, 4.65, 4.59, 4.40 BM

showing even more clearly the inverse effect of the spectrochemical series on the magnetic moment.

return to the CHEM2101 (C21J) course outline

Created and maintained by Prof. Robert J. Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.

Created Dec 1995. Links checked and/or last modified 12th October 2010.
URL http://wwwchem.uwimona.edu.jm/spectra/MagMoment.html